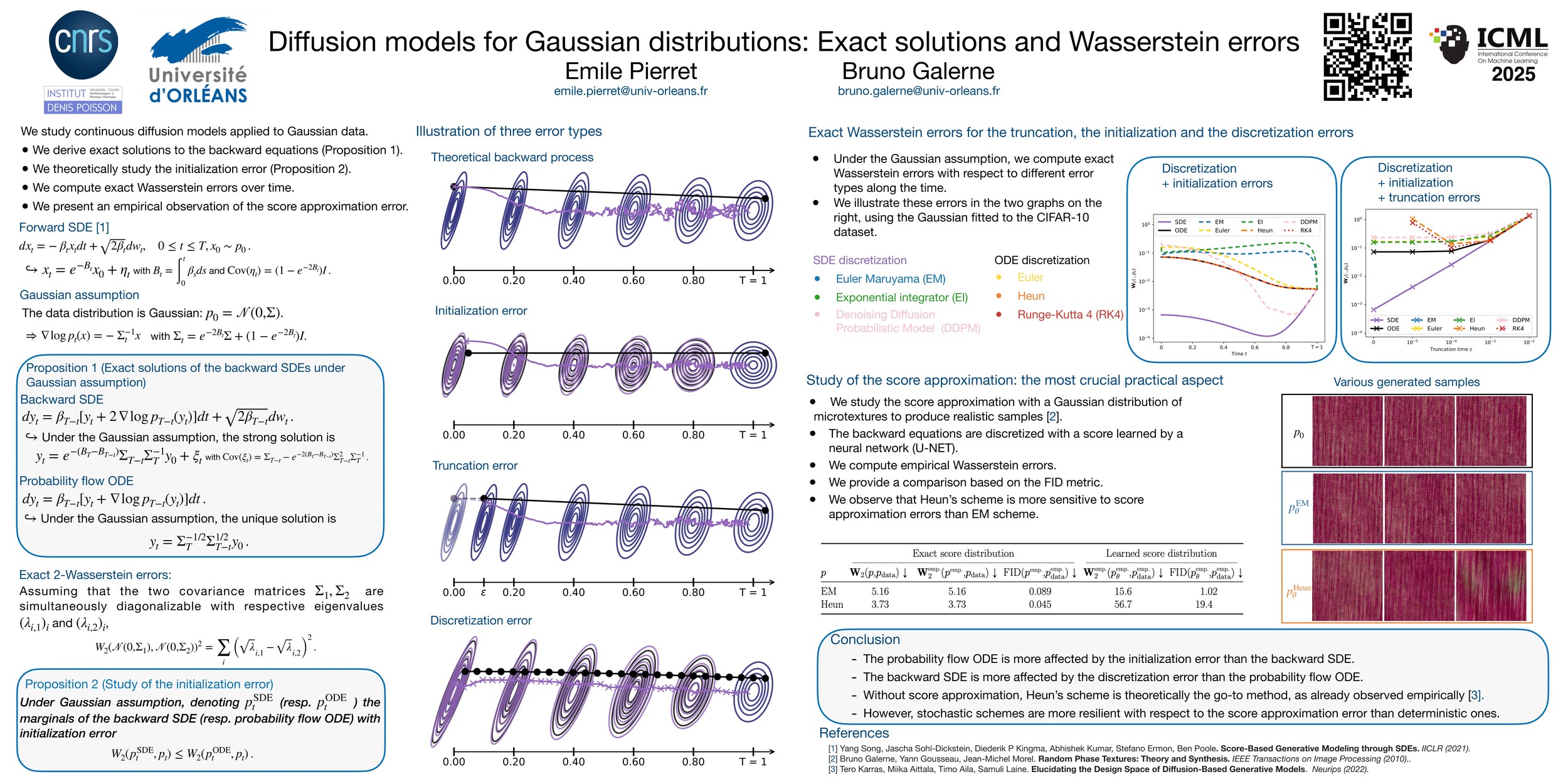
Abstract
Diffusion or score-based models recently showed high performance in image generation. They rely on a forward and a backward stochastic differential equations (SDE). The sampling of a data distribution is achieved by numerically solving the backward SDE or its associated flow ODE. Studying the convergence of these models necessitates to control four different types of error: the initialization error, the truncation error, the discretization error and the score approximation. In this paper, we theoretically study the behavior of diffusion models and their numerical implementation when the data distribution is Gaussian. Our first contribution is to derive the analytical solutions of the backward SDE and the probability flow ODE and to prove that these solutions and their discretizations are all Gaussian processes. Our second contribution is to compute the exact Wasserstein errors between the target and the numerically sampled distributions for any numerical scheme. This allows us to monitor convergence directly in the data space, while experimental works limit their empirical analysis to Inception features.
Background
We keep the same equation numbering as in the paper.
We study the continuous formulation of diffusion models, focusing on the Variance Preserving (VP-SDE) framework
[Song et al., 2021]. The forward process is:
\begin{equation} \label{eq:sde_forward} d\boldsymbol{x}_t =- \beta_t \boldsymbol{x}_t dt + \sqrt{2\beta_t}d\boldsymbol{w}_t, \quad 0 \leq t \leq T, \boldsymbol{x}_0 \sim p_{\text{data}}. \tag{1} \end{equation}
This degrades the data progressively. Denoting by $p_t$ the marginal distribution of $ \boldsymbol{x}_t$, we have $p_T$ close to $\mathcal{N}(0, I)$ if $\beta_t$ is properly chosen.
Theoretically, the reverse-time process
[Pardoux, 1986] is governed by the backward SDE:
\begin{equation} \label{eq:sde_backward} d{\boldsymbol{y}}_t = \beta_{T-t}[{\boldsymbol{y}}_t + 2 \nabla \log p_{T-t}({\boldsymbol{y}}_t)]dt + \sqrt{2\beta_{T-t}}d{\boldsymbol{w}}_t, \quad 0 \leq t < T, {\boldsymbol{y}}_0 \sim p_T \tag{2} \end{equation}
Or equivalently, the associated probability flow ODE:
\begin{equation} \label{eq:flow_reverse_ode} d{\boldsymbol{y}}_t = \beta_{T-t}\left[{\boldsymbol{y}}_t+ \nabla\log p_{T-t}({\boldsymbol{y}}_t)\right]dt, \quad 0 \leq t < T, {\boldsymbol{y}}_0 \sim p_T. \tag{5} \end{equation}
We illustrate this idea below: assuming that $p_{\text{data}}$ is Gaussian (left of the figure), the forward process evolves from left to right. The backward SDE (purple) and the probability flow ODE (black) reverse this evolution, with overlapping Gaussian ellipses in blue at each time step.

Error Types in Diffusion Models
We identify four distinct sources of error:
- Initialization error
- Truncation error
- Discretization error
- Score approximation error
Initialization Error
Occurs when the backward SDE or flow ODE is initialized with $\mathcal{N}(0,I)$ instead of the true $p_T$. This mismatch arises because $p_T$ is unknown in general. Although the forward process converges to $\mathcal{N}(0, I$ asymptotically, in practice we must use a finite $T$. This mismatch causes divergence between the SDE and ODE reverse marginals.

Truncation Error
This error results from stopping the reverse process at some small $\varepsilon > 0$ instead of time 0. It’s necessary when the data distribution lacks a density, e.g. if it’s supported on a manifold, making $\nabla \log p_t$ undefined at $t=0$.

Discretization Error
Discretizing the backward SDE or flow ODE is required for numerical simulation. The choice of discretization scheme (Euler, Heun, etc.) directly impacts the quality of the generated samples.

Score Approximation Error
In practice, the score function $\nabla \log p_t$ is unknown and approximated by a neural network $s_\theta$. This introduces a model approximation error. The success of diffusion models hinges on the quality of this learned score function.
Analysis Under Gaussian Assumption
To precisely analyze these errors, we focus on a tractable case:
Assumption (Gaussian assumption): $\quad p_{\text{data}} = \mathcal{N}(0, \boldsymbol{\Sigma}) $
This allows closed-form derivations. The covariance matrix $\boldsymbol{\Sigma}$ may be non-invertible, in which case the data lies on a manifold.
The exact score is given by:
\begin{equation} \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x}) = -\boldsymbol{\Sigma}_t^{-1} \boldsymbol{x} \end{equation}
where $ \boldsymbol{\Sigma}_t = e^{-\int_0^t \beta_s ds} \boldsymbol{\Sigma} + (1 - e^{-\int_0^t \beta_s ds}) I $.
Note: When $\boldsymbol{\Sigma} $ is singular, the score is undefined at $t = 0$, explaining the necessity of truncation.
In this Gaussian setting, we:
- Derive closed-form solutions for the backward SDE (Proposition 2)
- Solve the probability flow ODE exactly (Proposition 3)
- Compute exact Wasserstein-2 errors from initialization, truncation, and discretization (Section 4)
- Empirically study the score approximation error (Section 5)
Key Takeaways
- With only initialization error, the ODE sampler is more accurate than the SDE sampler (Proposition 4)
- Adding truncation and discretization errors, Heun’s method applied to the ODE yields the best performance (Figure 1)
- Score approximation is the most critical error in practice, and the SDE sampler is more robust to this noise
For full derivations and results, see the paper.
Bibtex
@inproceedings{Pierret_Galerne_diffusion_models_Gaussian_exact_solutions_errors_ICML2025,
title={Diffusion models for Gaussian distributions: Exact solutions and Wasserstein errors},
author={Emile Pierret and Bruno Galerne},
booktitle={Forty-second International Conference on Machine Learning},
year={2025},
}
References
[Song et al., 2021] Yang Song, Jascha Sohl-Dickstein, Diederik P Kingma, Abhishek Kumar, Stefano Ermon, & Ben Poole (2021). Score-Based Generative Modeling through Stochastic Differential Equations. In International Conference on Learning Representations.
[Pardoux, 1986] Pardoux, Étienne. Grossissement d'une filtration et retournement du temps d'une diffusion. Séminaire de probabilités, Tome 20 (1986), pp. 48-55.